La successione di Fibonacci
Lasciando in pace gli indaffarati conigli, cerchiamo di analizzare la sequenza dei numeri ottenuti, nota appunto come successione di Fibonacci, per la quale riportiamo di seguito i primi 25 termini:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025…
Le più immediate proprietà di tale successione sono:
ciascun termine è uguale alla somma dei due che lo precedono, ovvero, detto \(F_n\) l’ennesimo termine, risulta: \(F_{n} = F_{n-1} +F_{n-2}\);
due numeri consecutivi della successione sono primi fra loro;
se \(k\) è il M.C.D. di \(m\) ed \(n\), allora \(F_k\) è il M.C.D. di \(F_m\) e \(F_n\);
a somma dei primi \(n\) termini della successione è pari al termine \(F_{n+2}\) diminuito dell’unità: \(F_1 + F_2 + F_3 + \ldots +F_n = F_{n+2} \: – \: 1\);
la somma dei primi \(n\) termini di posto dispari è uguale al successivo termine della successione: \(F_1 + F_3 + F_5 + F_7 \ldots +F_{2n-1} = F_{2n}\);
la somma dei primi n termini di posto pari è uguale al successivo termine della successione diminuito dell’unità: \(F_2 + F_4 + F_6 + F_8 \ldots +F_{2n} = F_{2n+1} \: – \: 1\);
al crescere di \(n\), il rapporto tra l’ennesimo termine ed il precedente fornisce un’approssimazione via via migliore del numero aureo: infatti, per \(n = 5\), avremo \(5/3 = 1.6666\ldots\), per \(n=8\), \(21/13 = 1.6153\ldots\), per \(n = 11\), \(89/55 = 1.6181\ldots\), è da notare che tale metodo per il calcolo approssimato di \(\varphi\) fornisce gli stessi identici risultati del metodo delle frazioni continue prima accennato; p iù correttamente, per \(n\) che tende all’infinito, il rapporto tra l’ennesimo termine ed il precedente tende a \(\varphi\); di conseguenza, per \(n\) che tende all’infinito, la successione di Fibonacci tende ad una progressione geometrica di ragione \(\varphi\);
la somma dei quadrati dei primi \(n\) termini della successione è uguale al prodotto dell’ennesimo termine per il successivo: \(F_1^2 + F_2^2 + F_3^2 + \ldots +F_n^2 = F_n \cdot F_{n+1}\);
la somma dei quadrati di due termini consecutivi della successione, \(F_n\) ed \(F_{n+1}\), è ancora un numero di Fibonacci (di posto dispari): in particolare \(F_n^2 + F_{n+1}^2 = F_{2n+1}\);
per una qualsiasi terna di numeri consecutivi della successione, la differenza tra il prodotto degli estremi ed il quadrato del termine intermedio assume alternativamente il valore di \(\pm 1\); e, per n che tende all’infinito, la serie di dette differenze tende necessariamente a 0;
la differenza dei quadrati degli estremi di una generica terna di numeri consecutivi è ancora un numero di Fibonacci (di posto pari), in particolare: \(F_{n+1}^2 - F_{n-1}^2 = F_{2n}\);
da quattro numeri consecutivi della successione si ricava, invece, una terna pitagorica; il primo termine della terna si ottiene dal prodotto degli estremi, il secondo, dal doppio prodotto dei medi ed il terzo, l’ipotenusa, dalla somma dei quadrati dei medi. Quest’ultimo numero, come già detto, è esso stesso un numero di Fibonacci ed occupa, nella successione, un posto dispari, con esclusione, chiaramente, del primo e del terzo; provare per credere;
sommando un numero dispari di prodotti di successivi numeri di Fibonacci otteniamo il quadrato avente per lato l’ultimo termine della successione utilizzato; la rappresentazione geometrica di tale ultima proprietà è apprezzabile per la sua immediatezza: accanto al quadrato \(1 \times 1\) relativo alla prima coppia della successione, riportiamo, come in Fig. 4, il rettangolo \(1 \times 2\) della seconda coppia e su di essi adagiamo il rettangolo individuato dalla terza coppia \(2 \times 3\), ottenendo così il quadrato di lato 3; ripetendo l’operazione con i rettangoli relativi alle due successive coppie, \(3 \times 5\) e \(5 \times 8\), avremo il quadrato di lato 8, poi il quadrato di lato 21, e così via di seguito.
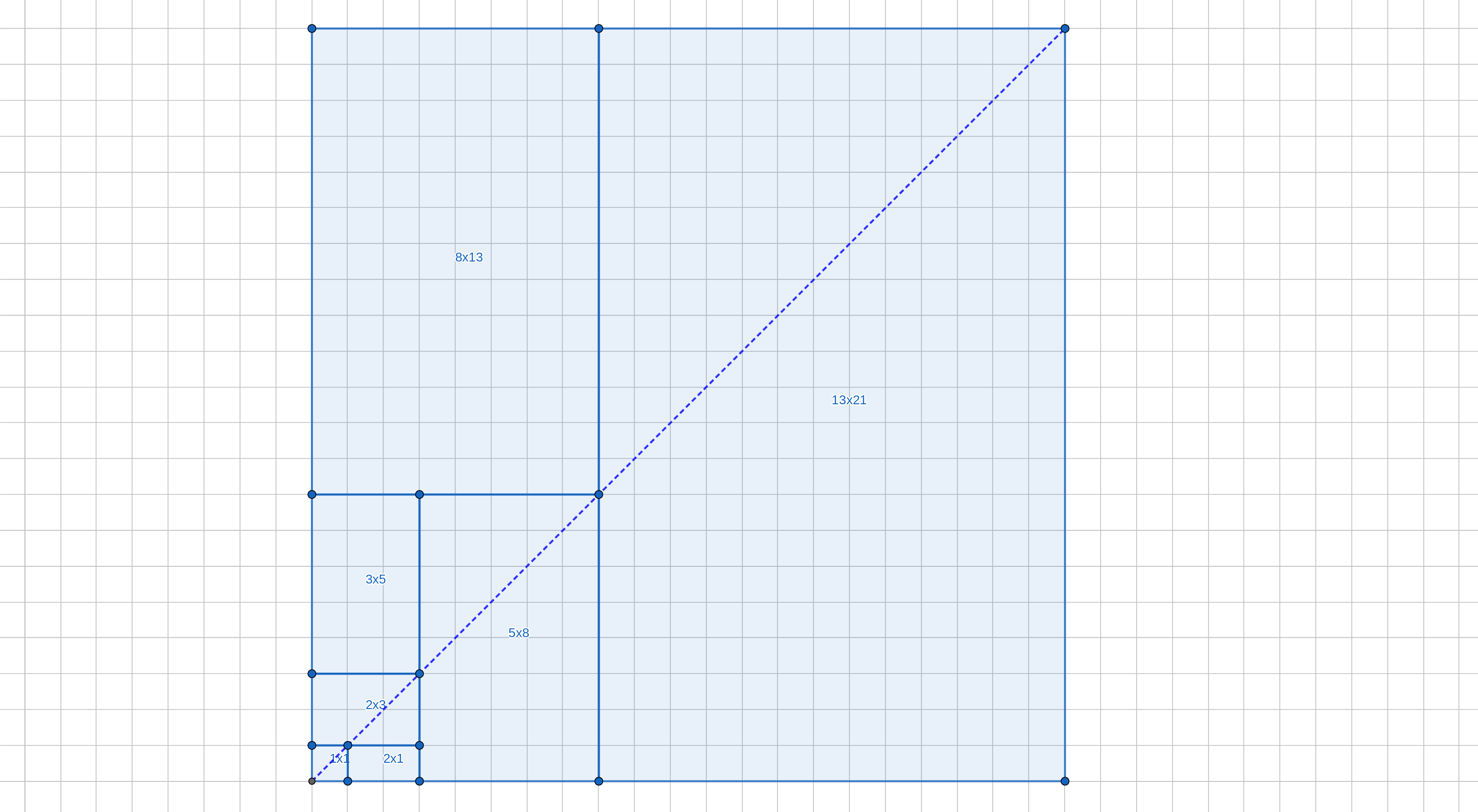
Fig. 4 Quadrati.
Riportiamo infine una formula che ci consente di calcolare l’ennesimo termine della successione:
Detta formula - già di per se strana in quanto, a partire da numeri irrazionali, produce numeri interi - può essere ulteriormente semplificata in:
infatti, al crescere di \(n\), il termine \(\frac{1}{\varphi^n} = (\varphi -1)^n\) tende rapidamente a \(0\).