Il triangolo aureo

In effetti con le dimensioni di un segmento e della sua parte aurea, Fig. 1, possiamo ottenere due diversi triangoli, entrambi isosceli: uno avente per base il segmento dato e l’altro, la sezione aurea dello stesso segmento. Di tali due triangoli è detto aureo, per la sua maggiore eleganza, il secondo.

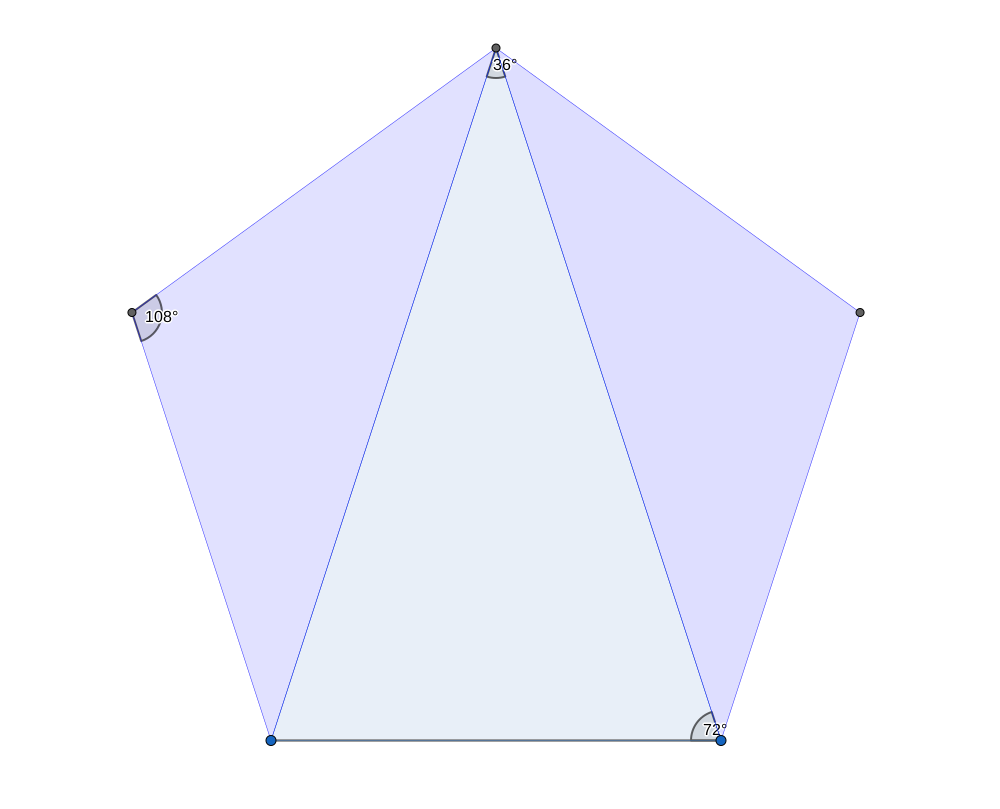
Fig. 3 I due triangoli aurei.

E, a proposito di eleganza, che dire della figura che si ottiene ada­giando lungo ciascuno dei due lati obliqui del nostro triangolo aureo il lato maggiore di due triangoli del primo tipo?

Non ci sono trucchi: trattasi proprio di un pentagono regolare dal quale, Fig. 3, possiamo facilmente dedurre:

1. il triangolo aureo è un triangolo isoscele con l’angolo al vertice pari ad 1/5 dell’angolo piatto, ovvero pari a 36°. Di conseguenza ciascuno dei due angoli alla base è pari a 72°;

2. in un qualsiasi pentagono regolare il lato è pari alla sezione au­rea della diagonale;

3. nello stesso pentagono regolare due diagonali non concorrenti nella stesso vertice si intersecano in un punto che le suddivide in due segmenti, il maggiore dei quali è ancora pari alla sezione aurea di ciascuna diagonale, ovvero al lato del pentagono;

4. per quanto alla precedente lettera a il lato di un decagono rego­lare è pari alla sezione aurea del raggio della circonferenza ad esso circoscritta.