La sezione aurea in natura
In una mezza mela, spaccata equatorialmente, fa bella mostra di sé un pentagono o, se si preferisce, una stella a cinque punte. Anche le pere hanno lo stesso vezzo. In proposito - fatto un cenno alla stella marina, alle foglie della vite, del platano e dell’acero, alla rosa canina, alla viola del pensiero, al gelsomino, ai fiori dell’arancio e del melo - si riporta, in Fig. 5, l’immagine di una petunia.

Fig. 5 Una petunia.
Le margherite ordinarie, quelle di m’ama - non m’ama, hanno 34 petali; sono comunque comuni anche margherite con 13, 21, 55 o 89 petali. Tutti numeri, ormai ben noti.

Fig. 6 Il centro (capolino) di una margherita.
Inoltre, la distribuzione delle infiorescenze al centro delle stesse margherite (capolino) può essere schematizzata come l’intersezione, Fig. 6 [1], di 34 spirali antiorarie con 21 spirali orarie, spirali logaritmiche, alle quali fanno capo, in due distinti ordini, i singoli petali.
Anche le infiorescenze nel capolino dei girasoli si distribuiscono come quelle delle margherite: apparentemente all’intersezione di 55 spirali antiorarie con 34 orarie ovvero, nel caso di girasoli molto grandi, all’intersezione di 144 spirali in un verso ed 89 nell’altro.
Le squame (brattee) della pigna di Fig. 7 [2] formano 8 spirali orarie e 13 antiorarie.
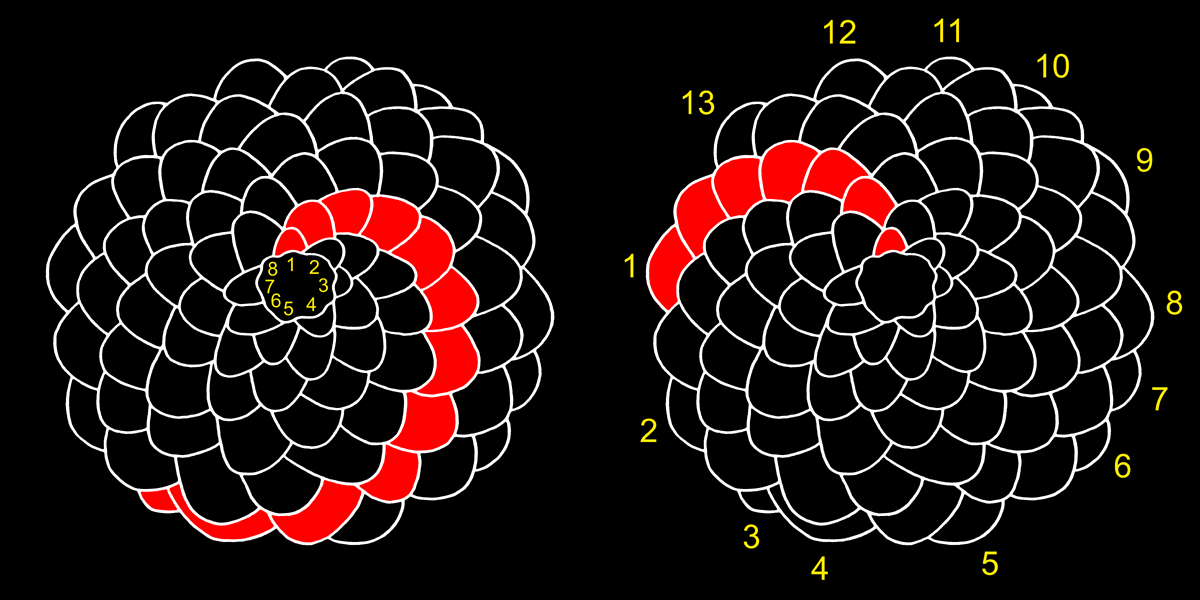
Fig. 7 La pigna.
Per l’ananas, le cui squame sono esagonali, la Fig. 8 [3] evidenzia 5 spirali leggermente ascendenti verso destra, 8 spirali ascendenti più rapidamente verso sinistra e 13 spirali decisamente ascendenti verso destra.

Fig. 8 L’ananas
Un cenno particolare spetterebbe anche al cavolo-broccolo romanesco. Ma il rischio di inciampare nei frattali è elevato, anzi immanente: preferiamo sorvolare.
Non sorvoliamo invece sulla spirale logaritmica (che condivide con i frattali la caratteristica dell’auto-similarità) descritta in natura, ad esempio, dalla conchiglia dei nautiloidi Fig. 9 [4], dalle corna dei montoni e dal volo del falco pellegrino quando,con il miglior assetto aerodinamico, si avventa sulla preda, senza perderla d’occhio.

Fig. 9 Conchiglia di nautiloide
Studiando in botanica la disposizione delle foglie su di un fusto, disciplina detta fillotassi o tassia fogliare, e limitandoci, per semplicità, al caso di una sola foglia per nodo, osserviamo che la successione delle foglie (infiorescenze, brattee, etc.) connessa all’accrescimento della pianta traccia un’elica immaginaria intorno al fusto (o ramo): in natura una nuova foglia, conto tenuto delle condizioni ambientali, non lascia mai la foglia precedente priva della pioggia, della luce e dell’aria necessarie al suo sviluppo ed alla sua vita!
E tale disposizione, tipica per ciascuna specie, può essere indicata dalla frazione fillotassica o quoziente di fillotassi, ovvero dal numero che esprime la frazione di angolo giro cui corrisponde l’angolo tra foglie successive. Più semplicemente il numeratore di detta frazione esprime il numero dei giri intorno al fusto necessari per un ciclo, ed il denominatore, il numero di foglie che si incontrano lungo l’immaginario percorso elicoidale per completare lo stesso ciclo.
E la frazione fillotassica (frazione di angolo giro) assume sempre e solo uno dei seguenti valori:
Trattasi, in tutta evidenza, di una nuova successione il cui generico termine, \(G_n\), risulta pari al rapporto tra il primo ed il terzo termine della generica terna di numeri consecutivi di Fibonacci:
E, per quanto detto in precedenza, tale rapporto, al crescere di \(n\), tende al valore di \(\frac{1}{\varphi^2} = 0.381866\ldots\)
Pertanto, l’angolo tra due foglie successive risulta rispettivamente pari a \(180^{\circ}\); \(120^{\circ}\); \(144^{\circ}\); \(135^{\circ}\); \(138,46^{\circ}\); \(137,14^{\circ}\); \(\ldots\); tendendo, al crescere di \(n\) (ovvero al diminuire della distanza internodale tra due foglie successive), all’angolo aureo sopra definito, pari a:
Come infatti si ricorderà, tale angolo è il minore dei due angoli nei quali l’angolo giro è suddiviso dal rapporto aureo, laddove il maggiore risulta pari a:
Madre natura è aurea? Certamente no. Sarebbe quantomeno riduttivo. Essa infatti è permeata di valori di gran lunga più preziosi dell’oro.
Note